| Population | |
| Clean | 9700 |
| Users | 300 |
| Total | 10000 |
| Population | Test negative | Test positive | |
| Clean | 9700 | 9506 | 194 |
| Users | 300 | 6 | 294 |
| Total | 10000 | 9512 | 488 |
| Population | Test negative | Test positive | |
| Clean | 9700 | 9506 | 194 |
| Users | 300 | 6 | 294 |
| Total | 10000 | 9512 | 488 |
| P = probability |  |
| A = "is a user" | |
| B = "tests positive" | |
| x|y = x, given y |
| P(A) = probability of being a user |  |
| P(B|A) = probability of testing positive, given being a user | |
| P(B) = probability of testing positive | |
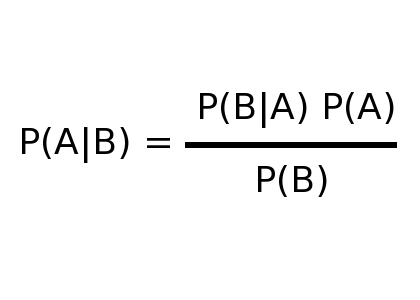
| P(A|B) = probability Bob's a user |
| P(A) = 3% |  |
| P(B|A) = probability of testing positive, given being a user | |
| P(B) = probability of testing positive | |
| P(A|B) = probability Bob's a user |
| P(A) = 3% |  |
| P(B|A) = 98% | |
| P(B) = probability of testing positive | |
| P(A|B) = probability Bob's a user |
| Population | Test negative | Test positive | |
| Clean | 9700 | 9506 | 194 |
| Users | 300 | 6 | 294 |
| Total | 10000 | 9512 | 488 |
| P(A) = 3% |  |
| P(B|A) = 98% | |
| P(B) = 4.88% | |
| P(A|B) = probability Bob's a user |
| P(A) = 3% |  |
| P(B|A) = 98% | |
| P(B) = 4.88% | |
| P(A|B) = (98% * 3%)/4.88% = 60.24% |