Write your own Bayesian Classifier!

John Melesky (Open Source Bridge, June 2009)

What's a Bayesian Classifier?

What's a Bayesian Classifier?

Something which classifies based on:

  1. Information about past categorizations
  2. Bayesian statistics (Bayes' Theorem)

What's Bayes' Theorem?

Let's check Wikipedia.

Derrr....

An example: random drug testing

3% of the population are using Zopadrine.

We have a drug test with a 98% accuracy rate.

An example: random drug testing

3% of the population are using Zopadrine.

We have a drug test with a 98% accuracy rate.

Bob is tested, and the result is positive. How likely is it that Bob uses Zopadrine?

Break it down

Let's assume a population of 10000 people.

Break it down

3% are users.

Population
Clean9700
Users300
Total10000

Break it down

The test is 98% accurate.

PopulationTest negativeTest positive
Clean97009506194
Users3006294
Total100009512488

Break it down

Bob is tested, and the result is positive. How likely is it that Bob uses Zopadrine?

PopulationTest negativeTest positive
Clean97009506194
Users3006294
Total100009512488

Break it down

294 / 488 = 60.24%

Back to Bayes' Theorem

Bayes' Theorem

Back to Bayes' Theorem

P = probability
A = "is a user"
B = "tests positive"
x|y = x, given y

Back to Bayes' Theorem

P(A) = probability of being a user
P(B|A) = probability of testing positive, given being a user
P(B) = probability of testing positive
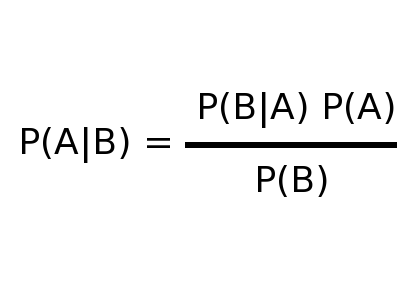
P(A|B) = probability Bob's a user

Back to Bayes' Theorem

P(A) = 3%
P(B|A) = probability of testing positive, given being a user
P(B) = probability of testing positive
P(A|B) = probability Bob's a user

Back to Bayes' Theorem

P(A) = 3%
P(B|A) = 98%
P(B) = probability of testing positive
P(A|B) = probability Bob's a user

Back to the numbers

PopulationTest negativeTest positive
Clean97009506194
Users3006294
Total100009512488

Back to Bayes' Theorem

P(A) = 3%
P(B|A) = 98%
P(B) = 4.88%
P(A|B) = probability Bob's a user

Back to Bayes' Theorem

P(A) = 3%
P(B|A) = 98%
P(B) = 4.88%
P(A|B) = (98% * 3%)/4.88% = 60.24%

This works with population numbers, too

P(A)   = 300
P(B|A) = 9800
P(B)   = 488
P(A|B) = 6024

Which is useful for reasons we'll see later.

Bayes' Theorem, in code

My examples are going to be in perl.

sub bayes {
  my ($p_a, $p_b, $p_b_a) = @_;

  my $p_a_b = ($p_b_a * $p_a) / $p_b;

  return $p_a_b;
}

Bayes' Theorem, in code

But you could just as easily work in Python.

def bayes(p_a, p_b, p_b_a):
  return (p_b_a * p_a) / p_b

Bayes' Theorem, in code

Or Java

public static Double bayes(Double p_a, Double p_b, Double p_b_a) {
  Double p_a_b = (p_b_a * p_a) / p_b;

  return p_a_b;
}

Bayes' Theorem, in code

Or SML

let bayes(p_a, p_b, p_b_a) = (p_b_a * p_a) / p_b

Bayes' Theorem, in code

Or Erlang

bayes(p_a, p_b, p_b_a) ->
  (p_b_a * p_a) / p_b.

Bayes' Theorem, in code

Or Haskell

bayes p_a p_b p_b_a = (p_b_a * p_a) / p_b

Bayes' Theorem, in code

Or Scheme

(define (bayes p_a p_b p_b_a)
  (/ (* p_b_a p_a) p_b))

Bayes' Theorem, in code

LOLCODE, anyone? Befunge? Unlambda?

If it supports floating point operations, you're set.

How does that make a classifier?

A = "is spam"
B = "contains the string 'viagra'"

What's P(A|B)?

What do we need for a classifier?

  1. We need to tokenize our training set
  2. Then build a model
  3. Then test that model
  4. Then apply that model to new data

What do we need for a classifier?

  1. We need to tokenize our training set
  2. Then build a model
  3. Then test that model
  4. Then apply that model to new data

Tokenizing your training set

Fancy perl

sub tokenize {
  my $contents = shift;

  my %tokens = map { $_ => 1 } split(/\s+/, $contents);
  return %tokens;
}

Tokenizing your training set

sub tokenize_file {
  my $filename = shift;

  my $contents = '';
  open(FILE, $filename);
  read(FILE, $contents, -s FILE);
  close(FILE);

  return tokenize($contents);
}

Tokenizing your training set

This is the "bag of words" model.

For each category (spam, not spam), we need to know how many documents in the training set contain a given word.

Tokenizing your training set

my %spam_tokens = ();
my %notspam_tokens = ();

foreach my $file (@spam_files) {
  my %tokens = tokenize_file($file);
  %spam_tokens = combine_hash(\%spam_tokens, \%tokens);
}

foreach my $file (@notspam_files) {
  my %tokens = tokenize_file($file);
  %notspam_tokens = combine_hash(\%notspam_tokens, \%tokens);
}

Tokenizing your training set

sub combine_hash {
  my ($hash1, $hash2) = @_;

  my %resulthash = %{ $hash1 };

  foreach my $key (keys(%{ $hash2 })) {
    if ($resulthash{$key}) {
      $resulthash{$key} += $hash2->{$key};
    } else {
      $resulthash{$key} = $hash2->{$key};
    }
  }

  return %resulthash;
}

What do we need for a classifier?

  1. We need to tokenize our training set
  2. Then build a model
  3. Then test that model
  4. Then apply that model to new data

Build a model

my %total_tokens = combine_hash(\%spam_tokens, \%notspam_tokens);

my $total_spam_files = scalar(@spam_files);
my $total_notspam_files = scalar(@notspam_files);
my $total_files = $total_spam_files + $total_notspam_files;
my $probability_spam = $total_spam_files / $total_files;
my $probability_notspam = $total_notspam_files / $total_files;

Build a model

In this case, our model is just a bunch of numbers.

Build a model

In this case, our model is just a bunch of numbers.

(a little secret: it's all a bunch of numbers)

What do we need for a classifier?

  1. We need to tokenize our training set
  2. Then build a model
  3. Then test that model
  4. Then apply that model to new data

*cough* *cough*

What do we need for a classifier?

  1. We need to tokenize our training set
  2. Then build a model
  3. Then test that model
  4. Then apply that model to new data

Apply that model to new data

my %test_tokens = tokenize_file($test_file);

foreach my $token (keys(%test_tokens)) {
  if (exists($total_tokens{$token})) {
    my $p_t_s = (($spam_tokens{$token} || 0) + 1) /
                ($total_spam_files + $total_tokens);
    $spam_accumulator = $spam_accumulator * $p_t_s;

    my $p_t_ns = (($notspam_tokens{$token} || 0) + 1) /
                 ($total_notspam_files + $total_tokens);

    $notspam_accumulator = $notspam_accumulator * $p_t_ns;
  }
}

Apply that model to new data

my $score_spam = bayes( $probability_spam,
                        $total_tokens,
                        $spam_accumulator );

my $score_notspam = bayes( $probability_notspam,
                           $total_tokens,
                           $notspam_accumulator );

my $likelihood_spam = $score_spam / ($score_spam + $score_notspam);
my $likelihood_notspam = $score_notspam / ($score_spam + $score_notspam);

printf("likelihood of spam email: %0.2f %%\n", ($likelihood_spam * 100));

Boom

What sucks?

What sucks?

What sucks?

What sucks?

Improve memory use

Limit the number of tokens

We want to use the tokens with the highest information values. That means tokens that are predominantly in one category but not the other.

Improve memory use

Limit the number of tokens

We want to use the tokens with the highest information values. That means tokens that are predominantly in one category but not the other.

There are a bunch of ways to calculate this, though the big one is Information Gain.

Improve tokenization, simple stuff

Improve tokenization, advanced stuff

Stemming

"wrestling", "wrestler", "wrestled", and "wrestle" are all the same word concept.

Pros: fewer tokens, related tokens match

Cons: some words are hard to stem correctly (e.g. "cactus")

Improve tokenization, advanced stuff

Include bigrams

Bigrams are token pairs. For example, "open source", "ron paul", "twitter addict".

Pros: we start distinguishing between Star Wars and astronomy wars

Cons: our memory use balloons

Improve tokenization, advanced stuff

Use numbers

Instead of binary (word x is in doc y), we store frequencies (word x appears z times in doc y).

Pros: damage from weak associations is reduced; easier to find the important words in a document

Cons: the math becomes more complex; in many cases, accuracy doesn't actually increase

Improve tokenization, advanced stuff

Use non-token features

Sometimes we want to use non-textual attributes of documents. For example, length of document, percent of capital letters.

Improve tokenization, advanced stuff

Use non-token features

Sometimes we want to use non-textual attributes of documents. For example, length of document, percent of capital letters.

We can also grab structural information, like the sender, or subject line, and treat them differently. Or whether the word appears early or late in the document.

Improve tokenization, advanced stuff

Use non-token features

Sometimes we want to use non-textual attributes of documents. For example, length of document, percent of capital letters.

We can also grab structural information, like the sender, or subject line, and treat them differently. Or whether the word appears early or late in the document.

Pros: a little can go a long way

Cons: selecting these can be a dark art. or an incredible memory burden.

Which leads us to

Which leads us to

Tokenization == Vectorization

In other words

Our documents are all just vectors of numbers.

Or even

Our documents are all just points in a high-dimensional Cartesian space.

Vectors of numbers

This concept opens up a whole world of statistical methods for categorization, including decision trees, linear separations, and support vector machines.

Points in space

And this opens up a whole different world of geometric methods for categorization and information manipulation, including k-nearest-neighbor classification and various clustering algorithms.

Alright

It's been a long trip. Any questions?

Thanks

Thanks for coming. Thanks to OS Bridge for having me.