Support Vector Machines
(lightning talk)
(LPW '07) (john melesky)
---
Presupposing:
- You have a bunch of something.
- You can transform relevant attributes of those things into numbers.
- You can connect those numbers into vectors (think coordinates in an attribute space).
- You want to categorise them base on those numbers.
---
The problem: find a line that separates these two categories of thing
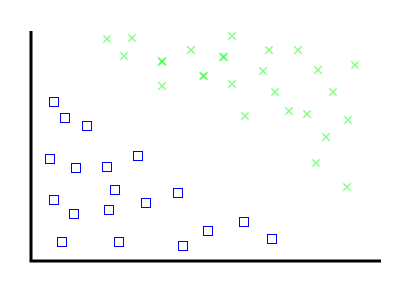 ---
For humans, this is easy.
---
For humans, this is easy.
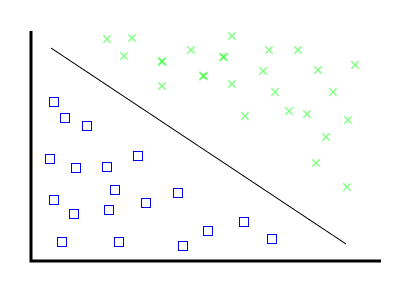 For mathematicians, it's actually not too hard.
---
For humans, this is easy.
For mathematicians, it's actually not too hard.
---
For humans, this is easy.
 For
For mathematicians computers, it's actually not too hard.
---
There are two problems, though.
---
Problem, the first:
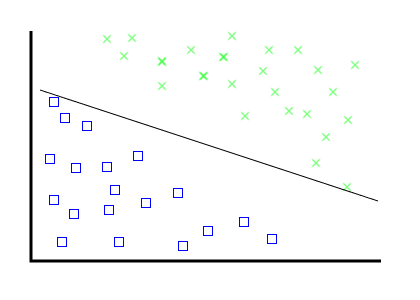 ---
Problem, the first:
---
Problem, the first:
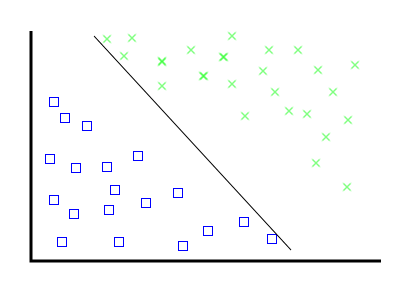 ---
Problem, the second:
---
Problem, the second:
 ---
Problem, the second:
---
Problem, the second:
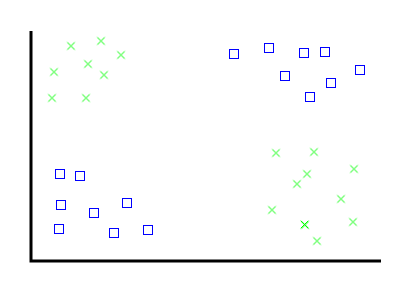 ---
Problem, the second:
---
Problem, the second:
 ---
Conveniently, Support Vector Machines address both of the problems i've identified.
---
Solution, the first:
---
Solution, the first:
---
Conveniently, Support Vector Machines address both of the problems i've identified.
---
Solution, the first:
---
Solution, the first:
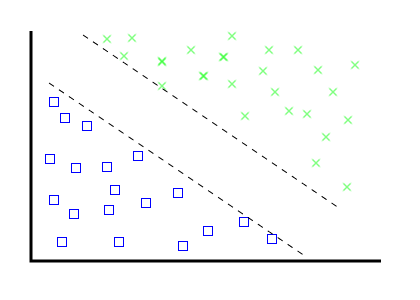
- Create "border" vectors, parallel to eachother, touching the outermost edge of each category dataset.
---
Solution, the first:

- Create "border" vectors, parallel to eachother, touching the outermost edge of each category dataset.
- As you add new items, ensure these "borders" stay parallel.
---
Solution, the first:
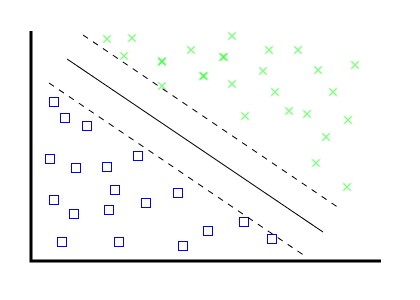
- Create "border" vectors, parallel to eachother, touching the outermost edge of each category dataset.
- As you add new items, ensure these "borders" stay parallel.
- Create your categorizing vector equidistant from your two "borders".
---
Solution, the first:

- Create "border" vectors, parallel to eachother, touching the outermost edge of each category dataset.
- As you add new items, ensure these "borders" stay parallel.
- Create your categorizing vector equidistant from your two "borders".
- These "borders" are called "support vectors".
---
A joke:
Q: How many mathematicians does it take to change a lightbulb?
---
A joke:
Q: How many mathematicians does it take to change a lightbulb?
A: One, who hands it to 127 Londoners, thus reducing it to an earlier joke.
---
A question:
Q: How do mathematicians categorize non-linearly-separable data?
---
A question:
Q: How do mathematicians categorize non-linearly-separable data?
A: Munge the data until it's linearly separable, thus reducing it to an earlier slide.
---
A question:
Q: How do mathematicians categorize non-linearly-separable data?
A: Munge the data until it's linearly separable, thus reducing it to an earlier slide.
Seriously. The munging is done using what are known as "kernel methods".
---
Kernel Methods
- Functions that munge data
- Very faintly magical (because i have no idea how they were derived)
- Require some skill to choose the right one for the problem
---
Kernel Methods + Support Vectors = Support Vector Machines
---
In Perl:
Algorithm::SVM - bindings to libsvm
(Also wrapped by AI::Categorizer)
 ---
For humans, this is easy.
---
For humans, this is easy.
 For mathematicians, it's actually not too hard.
---
For humans, this is easy.
For mathematicians, it's actually not too hard.
---
For humans, this is easy.
 For
For  ---
Problem, the first:
---
Problem, the first:
 ---
Problem, the second:
---
Problem, the second:
 ---
Problem, the second:
---
Problem, the second:
 ---
Problem, the second:
---
Problem, the second:
 ---
Conveniently, Support Vector Machines address both of the problems i've identified.
---
Solution, the first:
---
Solution, the first:
---
Conveniently, Support Vector Machines address both of the problems i've identified.
---
Solution, the first:
---
Solution, the first:



