|
|
@@ -0,0 +1,301 @@
|
|
|
+---
|
|
|
+title: Different Measures of Distance
|
|
|
+tags: geometry
|
|
|
+description: A few different ways of calculating distance in noncontinuous 2d spaces
|
|
|
+---
|
|
|
+
|
|
|
+How far is it from one place to another? How does that change if
|
|
|
+you're on a flat plane? What if that plane has discrete distances,
|
|
|
+like a checkerboard, or Civ map, or pixels on a screen?
|
|
|
+
|
|
|
+If we've got two points, *how far do you have to move to get from one
|
|
|
+to the other?*
|
|
|
+
|
|
|
+
|
|
|
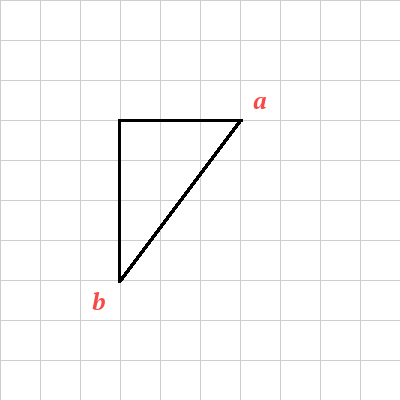
+### Euclidean Distance
|
|
|
+
|
|
|
+{width=150 height=150}
|
|
|
+
|
|
|
+This is the go-to of distance calculations. If you're talking about
|
|
|
+continuous, uniform planar (2d) space^[It holds for 3d and
|
|
|
+higher-dimensional spaces, too.], [Euclidean
|
|
|
+distance](https://en.wikipedia.org/wiki/Euclidean_distance) is the
|
|
|
+shortest distance between two points.
|
|
|
+
|
|
|
+In the most general sense, the way you get this distance is by
|
|
|
+measuring it. If you're lucky enough to be using [Cartesian
|
|
|
+coordinates](https://en.wikipedia.org/wiki/Cartesian_coordinate_system),
|
|
|
+then you can calculate the distance based on the distance between the
|
|
|
+two coordinate points. For our purposes, I'm going to use $a$ and $b$,
|
|
|
+located at $(x_1, y_1)$ and $(x_2, y_2)$.
|
|
|
+
|
|
|
+[Pythagoras](https://en.wikipedia.org/wiki/Pythagorean_theorem)
|
|
|
+figured out how to calculate the length of the hypotenuse of a right
|
|
|
+triangle. The fun part is that, with Cartesian coordinates, *any pair
|
|
|
+of points* can now define a right triangle. Just take one point with
|
|
|
+an x coordinate from one point and a y coordinate from the other, and
|
|
|
+the triangle itself can be defined as $((x_!, y_1), (x_1, y_2), (x_2,
|
|
|
+y_2))$^[Or $((x_!, y_1), (x_2, y_1), (x_2, y_2))$ if you're feeling
|
|
|
+frisky].
|
|
|
+
|
|
|
+At that point, it becomes pretty easy. The length of the two sides is
|
|
|
+just the absolute value of the difference between their x and y
|
|
|
+coordinates. So, $|x_1 - x_2|$ and $|y_1 - y_2|$. Those are easy to
|
|
|
+plug into the Pythagorean equation to get the distance between the
|
|
|
+points ($d$):
|
|
|
+
|
|
|
+$$d = \sqrt{ |x_1 - x_2|^2 + |y_1 - y_2|^2 }$$
|
|
|
+
|
|
|
+In code, this might look something like:
|
|
|
+
|
|
|
+~~~ { .python }
|
|
|
+def eucliddistance(x1, y1, x2, y2):
|
|
|
+ xdist = abs(x1 - x2)
|
|
|
+ ydist = abs(y1 - y2)
|
|
|
+ return math.sqrt( (xdist ** 2) + (ydist ** 2) )
|
|
|
+~~~
|
|
|
+
|
|
|
+This all seems a bit unnecessary, though, right? Cartesian coordinates
|
|
|
+are universal. They're how we think about points. All of our screens
|
|
|
+are Cartesian planes, and even our 3d worlds are Cartesian. Done and
|
|
|
+done.
|
|
|
+
|
|
|
+Still, I think it's good to appreciate how we got here. Why? **Because
|
|
|
+it doesn't work for our purposes.**
|
|
|
+
|
|
|
+[{width=150 height=150}](/images/post_2016_08_25/euclid_voronoi.png)
|
|
|
+
|
|
|
+A "point", to Euclid, is infinitesimal -- it has no size, nor
|
|
|
+shape. And a Euclidean plane is continuous -- there is no "smallest
|
|
|
+distance" you can move.
|
|
|
+
|
|
|
+Pixels, and graph squares, on the other hand, take up space. And if
|
|
|
+you want to get from $(0,0)$ to $(7,14)$ on a discrete plane, there's
|
|
|
+no such thing as moving 15.56247..... That's the nature of a discrete
|
|
|
+space -- everything's an integer. And the other fun bit is that you
|
|
|
+can't move in arbitrary directions. On a square grid, you've only got
|
|
|
+8 directions to go, at most.
|
|
|
+
|
|
|
+It is also, frankly, a bit costly to calculate. Square roots are a bit
|
|
|
+more complicated than adding and subtracting.
|
|
|
+
|
|
|
+Still, Euclidean distance is the definition of distance. And though we
|
|
|
+can't use it to determine distance of movement, we can still use it
|
|
|
+for comparative purposes.
|
|
|
+
|
|
|
+#### Voronoi Diagrams
|
|
|
+
|
|
|
+For illustration purposes, I've decided to use [Voronoi
|
|
|
+diagrams](https://en.wikipedia.org/wiki/Voronoi_diagram). Voronoi
|
|
|
+diagrams are a way of splitting up planes around a set of sites, such
|
|
|
+that all points in the plane are associated with the closest site.
|
|
|
+
|
|
|
+The simplest, slowest possible way to generate such a diagram is to
|
|
|
+iterate over each pixel in an image, calculate the distance between
|
|
|
+that pixel and each site, sort the sites by distance, and assign that
|
|
|
+site to the pixel. So I coded that up. I've put that code [up on
|
|
|
+github](https://github.com/jmelesky/voronoi_example). Nothing fancy
|
|
|
+going on, I assure you.
|
|
|
+
|
|
|
+By looking at the Voronoi diagrams for the same set of sites, using
|
|
|
+different distance measures, we can get an appreciation for how those
|
|
|
+measures vary, and what their characteristics are.
|
|
|
+
|
|
|
+
|
|
|
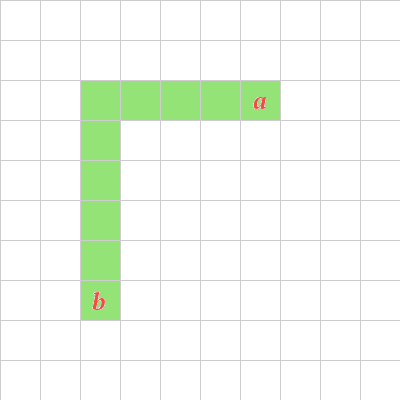
+### Manhattan Distance
|
|
|
+
|
|
|
+[{width=150 height=150}](/images/post_2016_08_25/taxi_voronoi.png)
|
|
|
+
|
|
|
+The island of Manhattan is densly populated, and densely built. For
|
|
|
+our purposes, though, it's also, notably, laid out like a grid. If you
|
|
|
+want to get two blocks up and two blocks over, you're going to have to
|
|
|
+move four total block lengths to get there. And that's a pretty
|
|
|
+straightforward distance measure.
|
|
|
+
|
|
|
+It's also known as taxicab distance, rectilinear distance, and a bunch
|
|
|
+of other things. And it's the simplest calculation we're going to be
|
|
|
+making. Just add the lengths of each side of our triangle:
|
|
|
+
|
|
|
+$$d = |x_1 - x_2| + |y_1 - y_2|$$
|
|
|
+
|
|
|
+In code, it might look like this:
|
|
|
+
|
|
|
+~~~ { .python }
|
|
|
+def taxidistance(x1, y1, x2, y2):
|
|
|
+ return (abs(x1 - x2) + abs(y1 - y2))
|
|
|
+~~~
|
|
|
+
|
|
|
+If you're on a checkerboard grid, and you are limited in movement to
|
|
|
+only the four cardinal directions, this is how you're going to measure
|
|
|
+getting from place to place. If you want to get from $(0,0)$ to
|
|
|
+$(7,14)$ in a taxi, you're going to go 21 squares, which is a fair bit
|
|
|
+further than 15.56.
|
|
|
+
|
|
|
+If you take a look at the Voronoi diagram derived from taxi distance,
|
|
|
+you'll see that the shapes have changed from straight-edged polygons
|
|
|
+to odd, almost art-deco-like shapes. In particular, some of the places
|
|
|
+where there were very long, thin cells in the Euclidean version have
|
|
|
+changed to blocky, angled, and often much distorted versions.
|
|
|
+
|
|
|
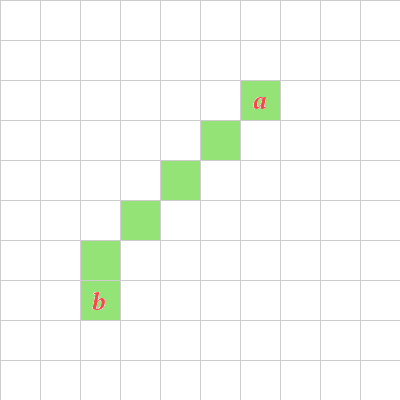
+### Civ Distance
|
|
|
+
|
|
|
+[{width=150 height=150}](/images/post_2016_08_25/civ_voronoi.png)
|
|
|
+
|
|
|
+If Manhattan distance is what you reckon with when you can only move
|
|
|
+in the four cardinal directions, what do you do when you can move in
|
|
|
+all 8 possible directions? Up until the most recent edition, the
|
|
|
+[Civilization games](https://en.wikipedia.org/wiki/Civilization_%28series%29) had
|
|
|
+exactly that scenario[^1]. So let's call this the Civ distance.
|
|
|
+
|
|
|
+Calculating this one is also easy. Instead of adding the sides
|
|
|
+together, you just take the length of the longest side.
|
|
|
+
|
|
|
+How's that work, exactly? Well, if you're going from $(0,0)$ to
|
|
|
+$(7,14)$, you go at an angle for 7 squares (moving twice as fast as
|
|
|
+taxicabs). At that point, you're at $(7,7)$, and it's a straight shot
|
|
|
+to $(7,14)$ only 7 squares away. Just 14 squares total.
|
|
|
+
|
|
|
+Mathematically, it looks like this:
|
|
|
+
|
|
|
+$$d = \max(|x_1 - x_2|, |y_1 - y_2|)$$
|
|
|
+
|
|
|
+And in code, something like this:
|
|
|
+
|
|
|
+~~~ {.python}
|
|
|
+def civdistance(x1, y1, x2, y2):
|
|
|
+ return (max(abs(x1 - x2), abs(y1 - y2)))
|
|
|
+~~~
|
|
|
+
|
|
|
+Again, very simple. And 14 is actually shorter than 15.56. By taxi, up
|
|
|
+and over is a distance of two, by Euclid that same distance is 1.41
|
|
|
+and change. But by Civ distance, that same span is only one. That, of
|
|
|
+course leads to some different distortions in the voronoi
|
|
|
+diagram. Where the taxicab Voronoi cells stretched up, down, left, and
|
|
|
+right, the Civ cells are stretching further in the diagonals.
|
|
|
+
|
|
|
+Overall, Civ distance is truer to Euclid than taking the taxi, but
|
|
|
+it's still a very different beast.
|
|
|
+
|
|
|
+### D&D Distance
|
|
|
+
|
|
|
+Perhaps you've played some Dungeons & Dragons. Perhaps you've
|
|
|
+specifically played 3.5ed^[Or its offshoot, Pathfinder; or, for that
|
|
|
+matter, any of the d20 games that also derived from that source]. That
|
|
|
+game was notorious for its complex, tactical, grid-based combat
|
|
|
+system. Each square represented 5 feet of space, and each character
|
|
|
+had a limited amount of movement per turn.
|
|
|
+
|
|
|
+[{width=150 height=150}](/images/post_2016_08_25/dandd_voronoi.png)
|
|
|
+
|
|
|
+Now, it didn't make sense to allow only movement in the four cardinal
|
|
|
+directions. That would, if nothing else, be incredibly frustrating for
|
|
|
+players trying to move their characters around the map.
|
|
|
+
|
|
|
+They also didn't want to allow willy-nilly Civ-style movement, since
|
|
|
+that would offer a clear advantage to anyone who wished to use the
|
|
|
+diagonals[^4ed].
|
|
|
+
|
|
|
+Ultimately, they decided on an iterative process which was a bit more
|
|
|
+complex:
|
|
|
+
|
|
|
+ - The first time (and every odd time) you move a diagonal, it costs
|
|
|
+ 5 feet of movement/distance, just like moving in a cardinal
|
|
|
+ direction
|
|
|
+
|
|
|
+ - The second time (and every even time) you move a diagonal, it
|
|
|
+ costs 10 feet of movement/distance, like you're taking a taxicab
|
|
|
+
|
|
|
+The net result is that, if you start out moving diagonally only, it's
|
|
|
+5 feet, then 15, then 20, then 30, then 35, then 45, etc. Translating
|
|
|
+feet to grid square units, it's 1 unit, then 3, then 4, then 6, then
|
|
|
+7, then 9.
|
|
|
+
|
|
|
+That pattern, as it turns out, is the floor of 1.5 * the diagonal
|
|
|
+distance.
|
|
|
+
|
|
|
+To generalize that to more than just the purely diagonal, we figure
|
|
|
+out how much we can go straight, then do the rest diagonal, and add
|
|
|
+them together:
|
|
|
+
|
|
|
+$$d_1 = \max(|x_1 - x_2|, |y_1 - y_2|) - \min(|x_1 - x_2|, |y_1 - y_2|)$$
|
|
|
+$$d_2 = \lfloor 1.5 \times (\min(|x_1 - x_2|, |y_1 - y_2|))\rfloor$$
|
|
|
+$$d = d_1 + d_2$$
|
|
|
+
|
|
|
+And in code, that looks like this[^odd]:
|
|
|
+
|
|
|
+~~~ {.python}
|
|
|
+def dandddistance(x1, y1, x2, y2):
|
|
|
+ mindist = min(abs(x1 - x2), abs(y1 - y2))
|
|
|
+ maxdist = max(abs(x1 - x2), abs(y1 - y2))
|
|
|
+ return ((maxdist - mindist) + (1.5 * mindist))
|
|
|
+~~~
|
|
|
+
|
|
|
+Looking at the Voronoi diagram, this is easily the closest match to
|
|
|
+Euclid. And that's not surprsing, really. When Euclid things up and
|
|
|
+over is 1.41 and change, taxicabs and Civ think it's 2 and 1,
|
|
|
+respectively, D&D thinks it's (about) 1.5, which is much, much closer
|
|
|
+to the continuous distance. To get from $(0,0)$ to $(7,14)$ by way of
|
|
|
+D&D distance is 17, which is pretty close to the 15.56 of Euclid, and
|
|
|
+without the distortions of Civ.
|
|
|
+
|
|
|
+Of course, it's a bit more complex to calculate than Civ or taxi, but
|
|
|
+it doesn't require taking any square routes, which marks it as still
|
|
|
+computationally simpler than Euclid. And it's grid-native. The
|
|
|
+designers of 3.5 did a good job finding a relatively simple
|
|
|
+approximation for distance.
|
|
|
+
|
|
|
+### Conclusion
|
|
|
+
|
|
|
+And here we are at the end. Hopefully getting from point $a$ to point
|
|
|
+$b$ wasn't too rough, and I know I learned a thing or two on the way.
|
|
|
+
|
|
|
+Things get more complicated when you start measuring things in three
|
|
|
+dimensions. The D&D algorithm, particularly, is unlikely to scale well
|
|
|
+as you end up figuring out the appropriate values for each of the 26
|
|
|
+different directions you can go. Maybe I'll revisit this again.
|
|
|
+
|
|
|
+And let's not forget non-spatial distances! [Hamming
|
|
|
+distance](https://en.wikipedia.org/wiki/Hamming_distance) is
|
|
|
+particularly fun to think about. It has uses in small-scale AI tasks
|
|
|
+like autocorrect, as well as in very-large-dimension binary vector
|
|
|
+spaces[^duh]. I guess I'm saying that distances are fascinating
|
|
|
+things, and there's so much more to talk about.
|
|
|
+
|
|
|
+Thanks for bearing with me.
|
|
|
+
|
|
|
+
|
|
|
+[^1]: For an even longer time, the king piece on a chessboard had the
|
|
|
+exact same abilities, which is why this is probably more commonly
|
|
|
+known as "chessboard distance", or [Chebyshev
|
|
|
+distance](https://en.wikipedia.org/wiki/Chebyshev_distance), after
|
|
|
+Pafnuty Chebyshev, a 19th-century Russian mathematician. But I've
|
|
|
+played more Civ than chess, frankly.
|
|
|
+
|
|
|
+[^4ed]: When it came time to publish the 4th edition of D&D, however,
|
|
|
+they changed their mind on this. The complexity of the 3.5 distance
|
|
|
+calculation wasn't worth the verisimilitude, so they moved to using
|
|
|
+Civ distances instead. This decision also led to the infamous [square
|
|
|
+fireballs](http://diceofdoom.com/blog/2009/10/powergaming-understanding-area-of-effect-in-dnd4e/),
|
|
|
+but no system is perfect.
|
|
|
+
|
|
|
+[^odd]: You might notice that there isn't a `min` or `math.floor` call
|
|
|
+in that code. There was, for a bit, but it was generating [some
|
|
|
+strange artifacts](/images/post_2016_08_25/odd_dandd_voronoi.png),
|
|
|
+where strange striping was occurring. I suspect that's due to an odd
|
|
|
+quantizing effect, but haven't looked into it deeply. In the meantime,
|
|
|
+using the un-floored numbers produce a more coherent image.
|
|
|
+
|
|
|
+[^duh]:
|
|
|
+ *Obviously*
|
|
|
+
|
|
|
+ ...
|
|
|
+
|
|
|
+ For some machine learning tasks, you end up representing different
|
|
|
+ things in very large vector spaces (one dimension for each
|
|
|
+ "feature" you are keeping track of). In many cases, *binary*
|
|
|
+ features are more tractable and just as useful -- for example, you
|
|
|
+ might keep track of *whether* a certain word shows up in a
|
|
|
+ document, rather than *how many times* it shows up. When those two
|
|
|
+ situations coincide, Hamming distance becomes more palatable and
|
|
|
+ tractable than Euclidean distance.]
|
|
|
+
|